Patterns in the Fibonacci Sequence
a) For each number in the Fibonacci Sequence, add all the previous Fibonacci numbers. Is there a pattern to the results?
If you add all the previous numbers for each number of the Fibonacci sequence, 0,1,12,3,5,8,13,21.34... you would get, 1,2,4,7,12,20,33,54,88,144...
Comparing the two sequences there is evidently a pattern.
If you add all the numbers preceding any term n (tern #), the difference between n and the sum is equal to the sum of all the numbers preceding n-1
b) Add alternate Fibonacci numbers starting with 0, 1 and with 1, 2. Compare the results.
0, 1, 1, 2, 3, 5, 8, 13, 21, 34...
1, 2, 3, 5, 8, 13, 21, 34, 55, 89...
When adding the alternate Fibonacci numbers which for each series is formed by adding the latest two values inorder o get the next value in the sequence, it is seen that whatever value is started with, it will always end up having terms that are equal to the Golden Ration (1.68).
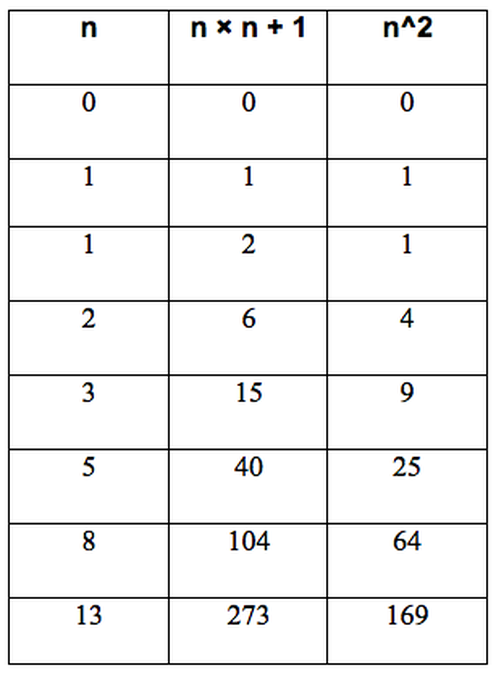
c) Create a table to record the following results. Multiply each Fibonacci number with the next one in the sequence. Multiply each Fibonacci number with itself. Add the squared Fibonacci numbers. Compare the results.
If you add all the previous numbers for each number of the Fibonacci sequence, 0,1,12,3,5,8,13,21.34... you would get, 1,2,4,7,12,20,33,54,88,144...
Comparing the two sequences there is evidently a pattern.
If you add all the numbers preceding any term n (tern #), the difference between n and the sum is equal to the sum of all the numbers preceding n-1
b) Add alternate Fibonacci numbers starting with 0, 1 and with 1, 2. Compare the results.
0, 1, 1, 2, 3, 5, 8, 13, 21, 34...
1, 2, 3, 5, 8, 13, 21, 34, 55, 89...
When adding the alternate Fibonacci numbers which for each series is formed by adding the latest two values inorder o get the next value in the sequence, it is seen that whatever value is started with, it will always end up having terms that are equal to the Golden Ration (1.68).
c) Create a table to record the following results. Multiply each Fibonacci number with the next one in the sequence. Multiply each Fibonacci number with itself. Add the squared Fibonacci numbers. Compare the results.
The pattern or formula that comes out of this particular situation is that
(an)^2 + (an + 1) ^2 = a2n
d) Create a table or list the first 30 numbers in the Fibonacci Sequence. Use different colors to shade the multiples of the Fibonacci numbers 2, 3, 5 and 8. Does a pattern emerge?
Key
Multiples of 2
Multiples of 3
Multiples of 5
Multiples of 8
First 30 Fibonacci Numbers
(an)^2 + (an + 1) ^2 = a2n
d) Create a table or list the first 30 numbers in the Fibonacci Sequence. Use different colors to shade the multiples of the Fibonacci numbers 2, 3, 5 and 8. Does a pattern emerge?
Key
Multiples of 2
Multiples of 3
Multiples of 5
Multiples of 8
First 30 Fibonacci Numbers
- 1
- 1
- 2 _
- 3 _
- 5 _
- 8 _ _
- 13
- 21 _
- 34 _
- 55 _
- 89
- 144 _ _
- 233
- 377
- 610 _
- 987 _
- 1,597
- 2,584 _ _
- 4,181
- 6,765 _ _
- 10,946 _
- 17,711
- 28,657
- 46,368 _ _ _
- 75,025 _
- 121,393
- 196,418 _
- 317,811 _
- 514,229
- 832,040 _ _ _
By doing this activity there was an evident pattern.
That of :
Every 3 terms is a multiple of 2
Every 4 terms is a multiple of 3
Every 5 terms is a multiple of 5
Every 6 terms is a multiple of 8
That of :
Every 3 terms is a multiple of 2
Every 4 terms is a multiple of 3
Every 5 terms is a multiple of 5
Every 6 terms is a multiple of 8